PARALLEL DELAUNAY TRIANGULATION
Tianyi Chen | Yuqi Gong

Summary
In this project, we implemented two parallel versions of Delaunay triangulation algorithm. The first one, based on an incremental insertion algorithm, doesn't achieve significant speedup due to limitation of platform and language choices. The second version builds off of that, and combines the idea from a modified divide-and-conquer algorithm. Using OpenMPI, it achieves 50x speedup when running with 64 cores at Pittsburgh Supercomputing center (PSC).
Background
Given a set of points on the plane, the Delaunay triangulation separates the plane by its convex hull (Remark: because of this, any algorithm that computes it should take at least Ω(nlogn) time.).
Inside the convex hull, it yields a triangulation such that no point lies inside the circumcircle of any triangle. The Delaunay triangulation exists if there are no three collinear points ”near each other”, and it is unique if no four ”nearby” points that lie on the same circle.
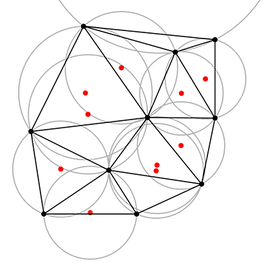
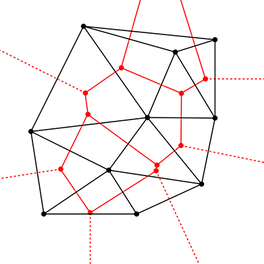

Parallel Incremental Insertion
Algorithm

Parallel Computing Module Choice
We choose OpenMP to enable this parallelism. Essentially, we want to distribute the triangles in the mesh equally to all the processors to achieve workload balance.
A major problem we encountered was that the triangles has to be stored as a set in C++ to enable constant time insertion and deletion. But the parallel for directive in openMP doesn't work on sets, because they have no constant time random iterator.
The first workaround we tried was to use the task directive. One thread iterate the set of triangles and spawn tasks, and the other threads handle them in the meantime. However, we suffer from the correctness and performance issues (which are discusses more in detail in the report). Eventually, we turned away from the task directive, and choose to copy the set of triangles into a vector at the beginning of each iteration. This solves the above problems and offers some observable speedup, but it also brings negative impacts to performance.
Results & Analysis

The biggest problem, as mentioned above, is we have to convert set to vector to enable parallel execution. Copying these data structures in each iteration actually constitutes a significant portion of the total work.
When running with 1 thread on the ghc81 machine, the sequential work takes 44.8% of entire time. Due to Amdahl's Law, this makes the best speedup about 2.
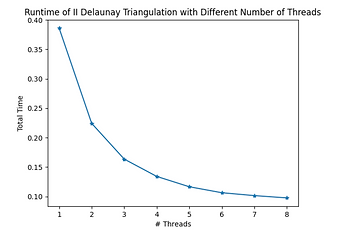
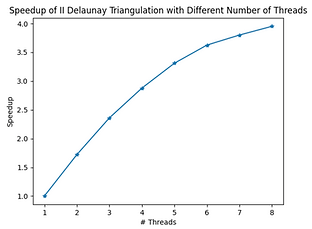
The speedup seems to level off pretty quickly. The best speedup is only 4x when using 8 cores. This made us question the scalability of this algorithm.

The blue bars represent the total runtime, while the yellow portion is spent on lock/unlock. The results are very consistent with our conjecture (the poor scalability is due to synchronization overhead). And the most important implication is that, without other optimizations, this algorithm won't achieve good speedup even if we get rid of the sequential portion!
Reflection
Even though we implement a correct version of the Delaunay triangulation that is algorithmically parallel, the practical speedup is unsatisfactory.
One reason is the slight incompatibility between unordered set in C++ and openMP parallel for directive.
The more important reason concerns synchronization overhead. Ideally, if we have a library that supports fine-grained locking, we believe that it could greatly improve overall speedup.
Nevertheless, since we're implementing everything from scratch, the single-thread version of this algorithm, which is work efficient, proves to be very helpful in the second algorithm we implement.

Algorithm
1. Let nproc be the number of processors.
2. Find the nproc − 1 points whose x-coordinates equally divide the input points
3. Processor i takes the i-th point (processor 0 does nothing), computes the Delaunay path using the projection method, and sends the path to the previous processor
4. Let rightPath be the received path, and leftPath be the computed path
5. Filter all points that lie between leftPath and rightPath. The first processor only considers its right path, and the last processor only considers its left path. All points on the path belong to both sections.
6. For each region, compute the Delaunay triangulation independently (using the sequential incremental insertion algorithm implemented in the first section).
7. Combine all the triangles from each region.

Parallel Computing Module Choice
We think a message passing model would work well with this algorithm, since each region is essentially handled by one core, computing its own Delaunay triangulation. The only communication needed is the boundary information with neighboring processors, as well as merging the final triangulation to one master processor. Therefore, we use the openMPI module to implement the algorithm and everything works pretty smoothly.
Results & Analysis
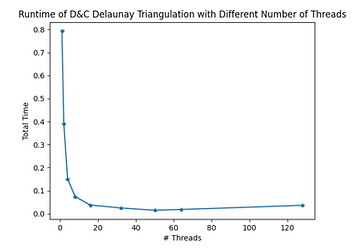
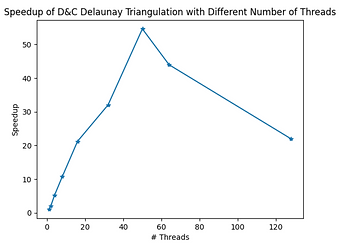
As shown in the above figures, the algorithm achieve very good speedup. While it takes the sequential version 0.8s to complete the computation, it takes less than 0.02s using 50 cores, making the maximum speedup almost 55x.
The only trade-off here is that as the number of processors grow, more boundaries have to be computed, increasing the total amount of work. This is reflected in the later half of the curve, where the execution time starts to curve back up and the speedup drops.
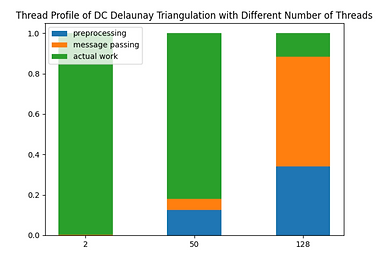
Clearly, when there are only 2 threads, almost all execution time is devoted to actual work. When there are 128 threads, however, the majority time is spent on preprocessing and message passing (each region is too small compared to the amount of preprocessing). The 50-thread case, where maximum speedup is achieved, is the sweet spot that balances parallelism and extra work.
Parallel Divide and Conquer
Reflection
Overall, this algorithm does really well in terms of utilizing parallel computing resources. We made some modifications to the original algorithm in order to reduce implementation complexity. Gladly, everything works out smoothly and satisfactory speedup is achieved. In retrospect, message passing model seems to be a suitable framework for this algorithm, and we don't think choosing GPU or any other platform would offer significant improvement.